Sökningar, diagram, statistik och pivottabeller

Efter att ha granskat grundläggande funktioner, cellreferenser och datum- och tidsfunktioner dyker vi nu in i några av de mer avancerade funktionerna i Microsoft Excel. Vi presenterar metoder för att lösa klassiska problem i finans, försäljningsrapporter, fraktkostnader och statistik.

SCHOOL NAVIGATION

1. Varför behöver du formler och funktioner?
2. Definiera och skapa en formel
3. Relativ och Absolut Cellreferens och Formatering
4. Användbara funktioner du bör lära känna
5. Sökningar, diagram, statistik och pivottabeller

Dessa funktioner är viktiga för företag, studenter och de som bara vill lära sig mer.

VLOOKUP och HLOOKUP

Här är ett exempel för att illustrera vertikala uppslag (VLOOKUP) och horisontella uppslag (HLOOKUP) -funktioner. Dessa funktioner används för att översätta ett tal eller annat värde till något som är förståeligt. Till exempel kan du använda VLOOKUP för att ta delnummer och returnera artikelbeskrivningen.

För att undersöka detta, låt oss gå tillbaka till vårt "Decision Maker" -kalkylblad i del 4, där Jane försöker bestämma vad som ska bäras i skolan. Hon är inte längre intresserad av vad hon bär, eftersom hon landat en ny pojkvän, så kommer hon nu att ha slumpmässiga kläder och skor.

I Janes kalkylblad listar hon kläder i vertikala kolumner och skor, horisontella kolumner.

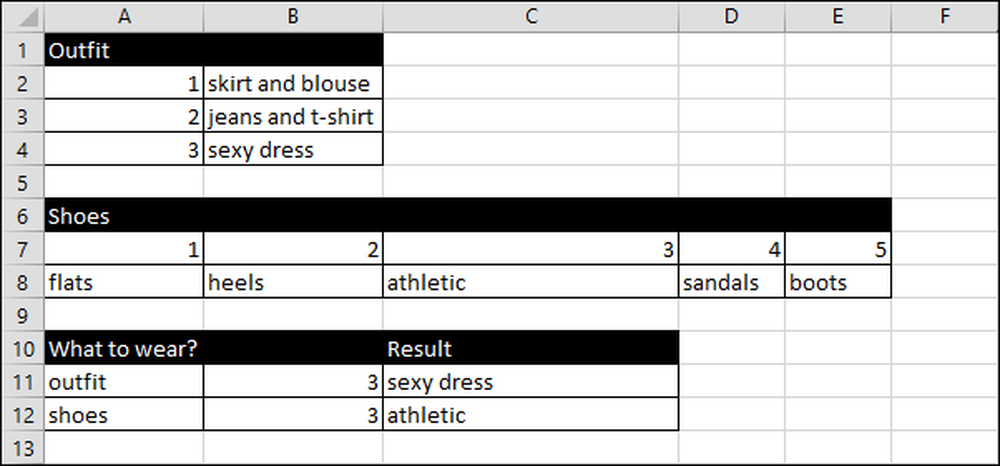
Hon öppnar kalkylbladet och funktionen RANDBETWEEN (1,3) genererar ett tal mellan eller lika med ett och tre som motsvarar de tre typerna av kläder som hon kan bära.

Hon använder funktionen RANDBETWEEN (1,5) för att välja mellan fem typer av skor.

Eftersom Jane inte kan bära ett nummer behöver vi konvertera detta till ett namn, så vi använder sökfunktioner.

Vi använder VLOOKUP-funktionen för att översätta klädnummeret till klädselnamnet. HLOOKUP översätter från skonnummer till olika typer av skor i raden.

Kalkylbladet fungerar så här för outfits:

Excel väljer ett slumptal från en till tre, eftersom hon har tre outfitalternativ.

Därefter översätter formeln numret till text med = VLOOKUP (B11, A2: B4,2) som använder slumpmässigt talet värdet från B11 att se inom intervallet A2: B4. Det ger då resultatet (C11) från de uppgifter som anges i andra kolumnen.

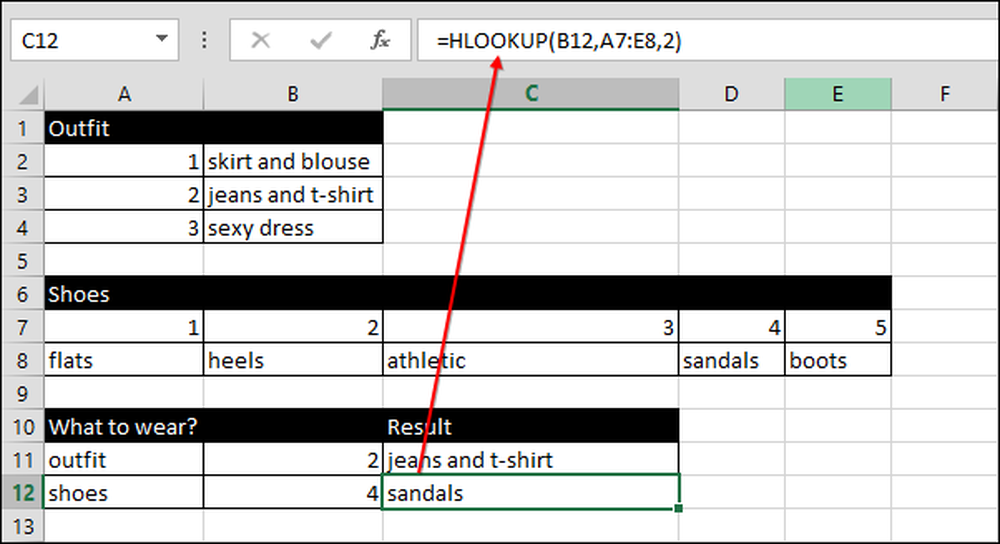
Vi använder samma teknik för att välja skor, förutom den här gången använder vi VOOKUP istället för HLOOKUP.

Exempel: Grundstatistik

Nästan alla vet en formel från statistiken - genomsnittet - men det finns en annan statistik som är viktig för verksamheten: standardavvikelse.

Till exempel, många en person som har gått på college har agonized över deras SAT poäng. De kanske vill veta hur de rankas jämfört med andra studenter. Universiteten vill också veta detta eftersom många universitet, särskilt prestigefyllda, slår ner elever med låga SAT-poäng.

Så hur skulle vi, eller ett universitet, mäta och tolka SAT-poäng? Nedan följer SAT-poäng för fem studenter som sträcker sig från 1.870 till 2.230.

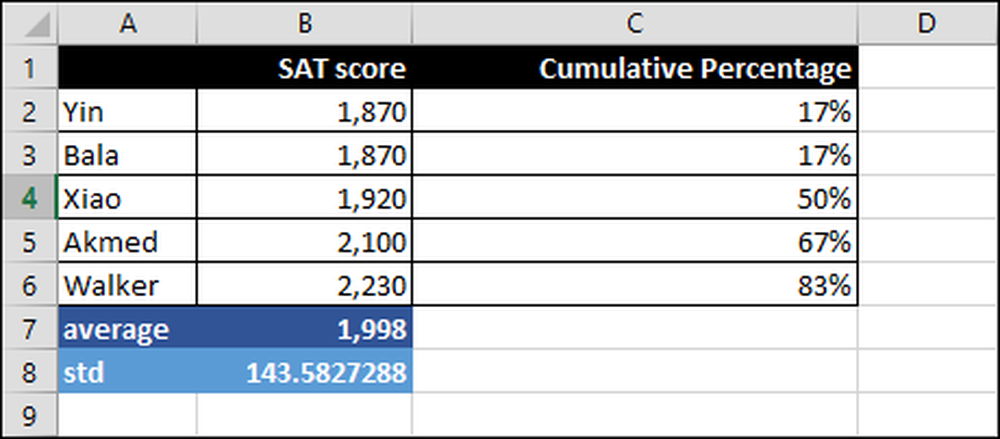
De viktiga siffrorna att förstå är:

Medel - Medel kallas också "medelvärdet".

Standardavvikelse (STD eller σ) - Det här numret visar hur stor mängd dispergerad en uppsättning siffror är. Om standardavvikelsen är stor, är siffrorna långt ifrån varandra och om det är noll är alla siffrorna desamma. Man kan säga att standardavvikelsen är den genomsnittliga skillnaden mellan medelvärdet och det observerade värdet, dvs 1,998 och varje SAT-poäng. Observera att det är vanligt att förkorta standardavvikelsen med den grekiska symbolen sigma "σ."

Procentuell ranking - När en elev får en hög poäng kan de skryta att de är i topp 99-procentilen eller något liknande. "Percentil rankning" betyder att procentandelen av poängen är lägre än ett visst poäng.

Standardavvikelsen och sannolikheten är nära kopplade. Du kan säga att för varje standardavvikelse är sannolikheten eller sannolikheten för att antalet ligger inom det antal standardavvikelser som är:

STD	Procentandel av poäng	Räckvidd av SAT-poäng
1	68%	1,854-2,142
2	95%	1,711-2,285
3	99,73%	1,567-2,429
4	99,994%	1,424-2,572

Som du kan se är chansen att någon SAT-poäng är utanför 3 STDs praktiskt taget noll eftersom 99,73 procent av poängen ligger inom 3 STDs.

Låt oss nu titta på kalkylbladet igen och förklara hur det fungerar.

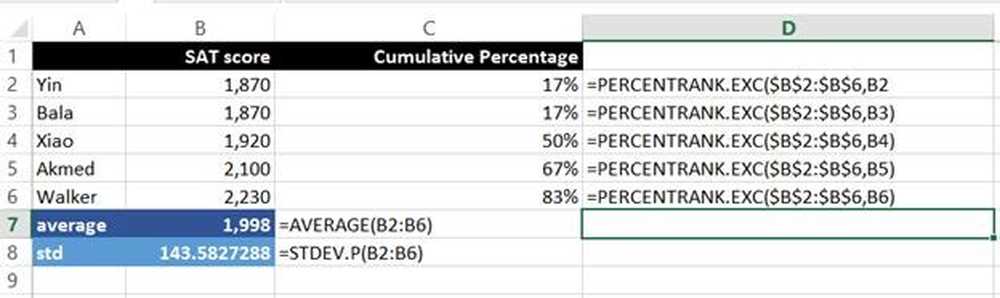
Nu förklarar vi formlerna:

= MEDEL (B2: B6)

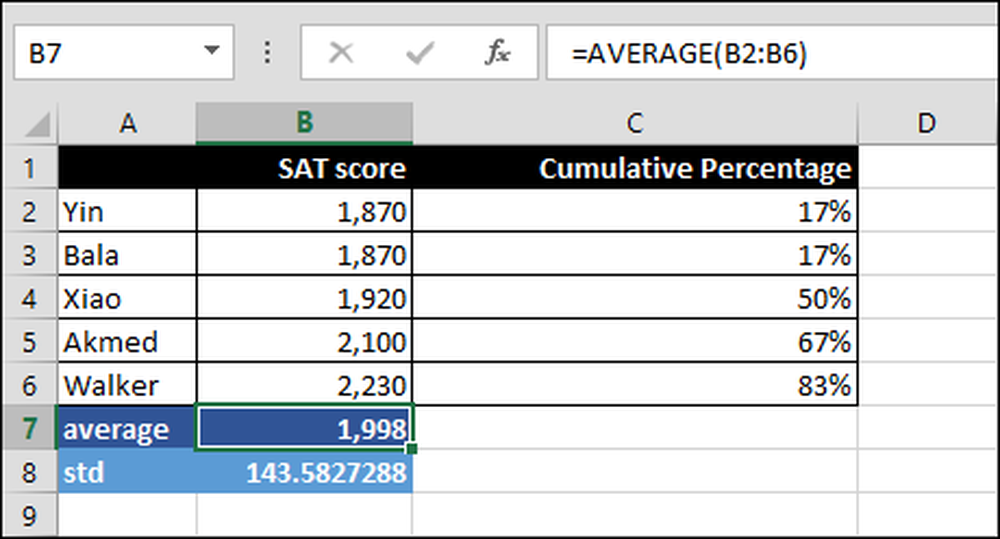
Medelvärdet av alla poäng över intervallet B2: B6. Specifikt summan av alla poäng dividerat med antalet personer som tog testet.

= STDEV.P (B2: B6)

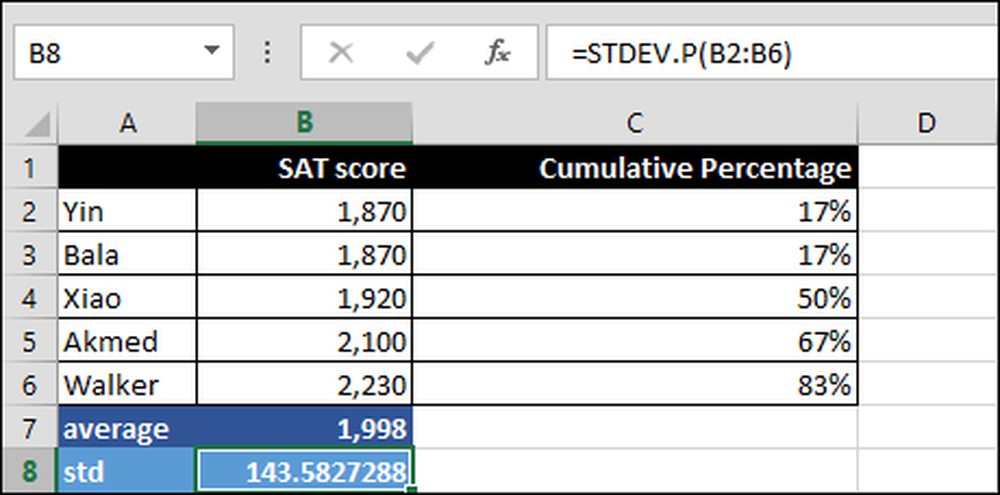
Standardavvikelsen över intervallet B2: B6. ".P" betyder STDEV.P används över alla poäng, dvs hela populationen och inte bara en delmängd.

= PERCENTRANK.EXC ($ B $ 2: $ B $ 6, B2)

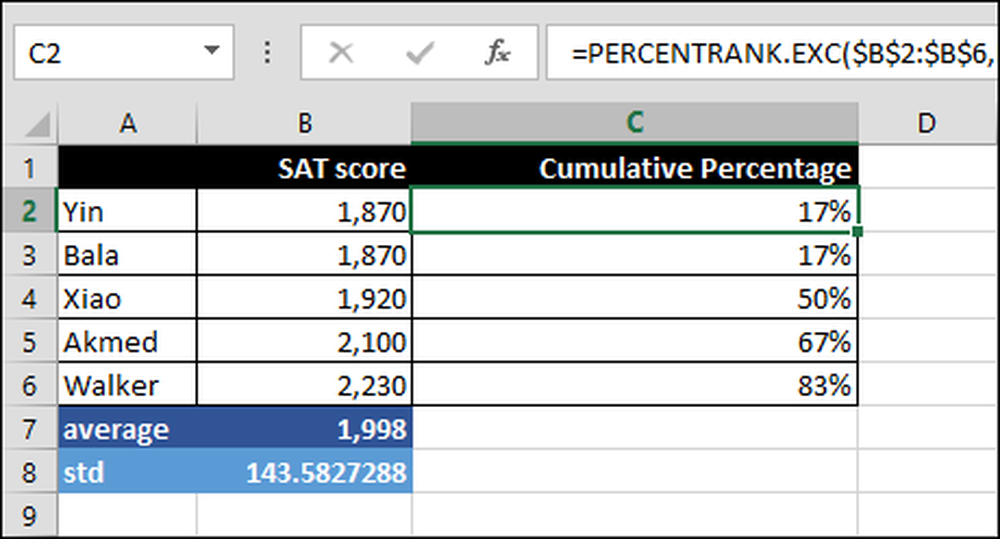
Detta beräknar den kumulativa procentsatsen över intervallet B2: B6 baserat på SAT-poängen, i detta fall B2. Till exempel ligger 83 procent av poängen under Walker's poäng.

Graferar resultaten

Att lägga resultaten i ett diagram gör det lättare att förstå resultaten, plus du kan visa det i en presentation för att göra din poäng tydligare.

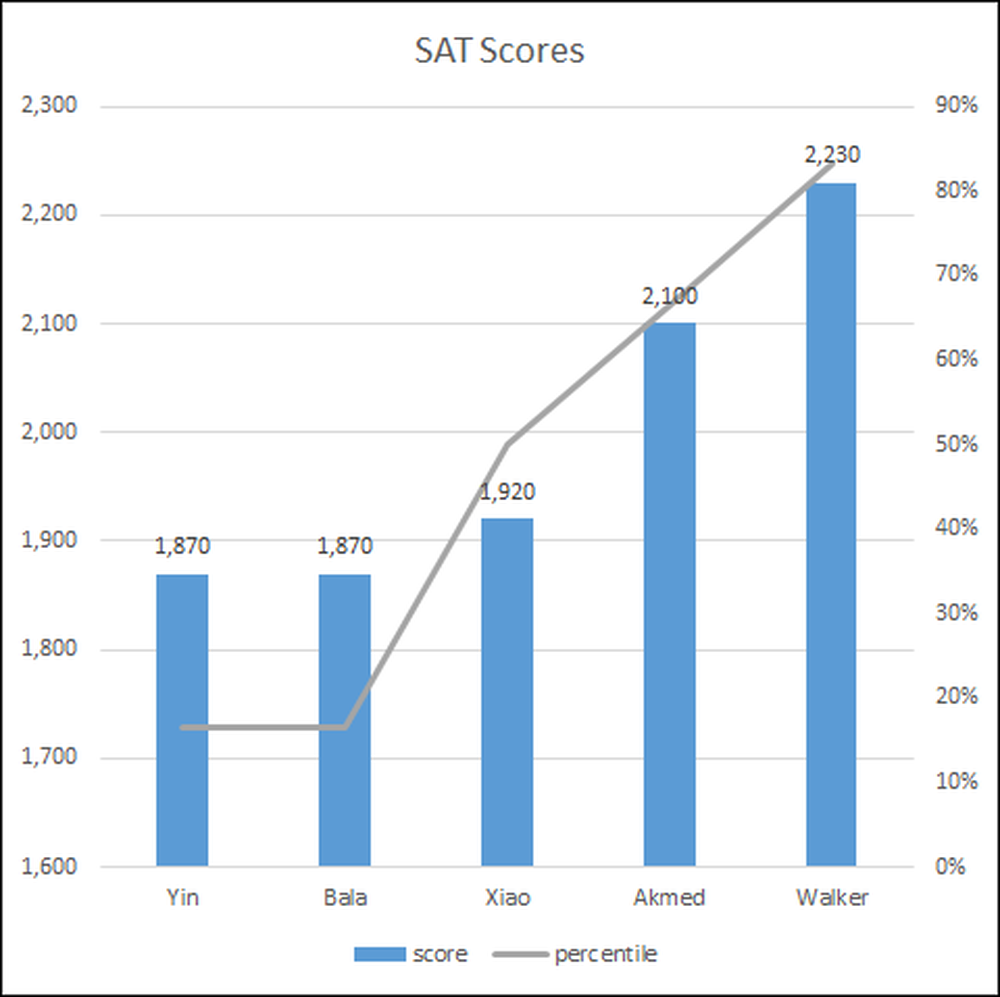
Eleverna ligger på den horisontella axeln och deras SAT-poäng visas som en blå stapeldiagram på en skala (vertikal axel) från 1600 till 2.300.

Den procentuella rankningen är den högra vertikala axeln från 0 till 90 procent och representeras av den grå linjen.

Så här skapar du en bild

Att skapa ett diagram är ett ämne för sig själv, men vi kommer att förklara kortfattat hur ovanstående diagram skapades.

Välj först cellintervallet i diagrammet. I det här fallet A2 till C6 eftersom vi vill ha numren samt studentens namn.

Från "Insert" -menyn välj "Diagram" -> "Rekommenderade diagram":

Datorn rekommenderar ett diagram med "Clustered-Column, Secondary Axis". Den "sekundära axeln" delen betyder att den drar två vertikala axlar. I det här fallet är detta diagram det vi vill ha. Vi behöver inte göra någonting annat.

Du kan använda flytta diagrammet runt och omforma det tills du har det som storlek och i önskad position. När du väl är nöjd kan du spara diagrammet i kalkylbladet.

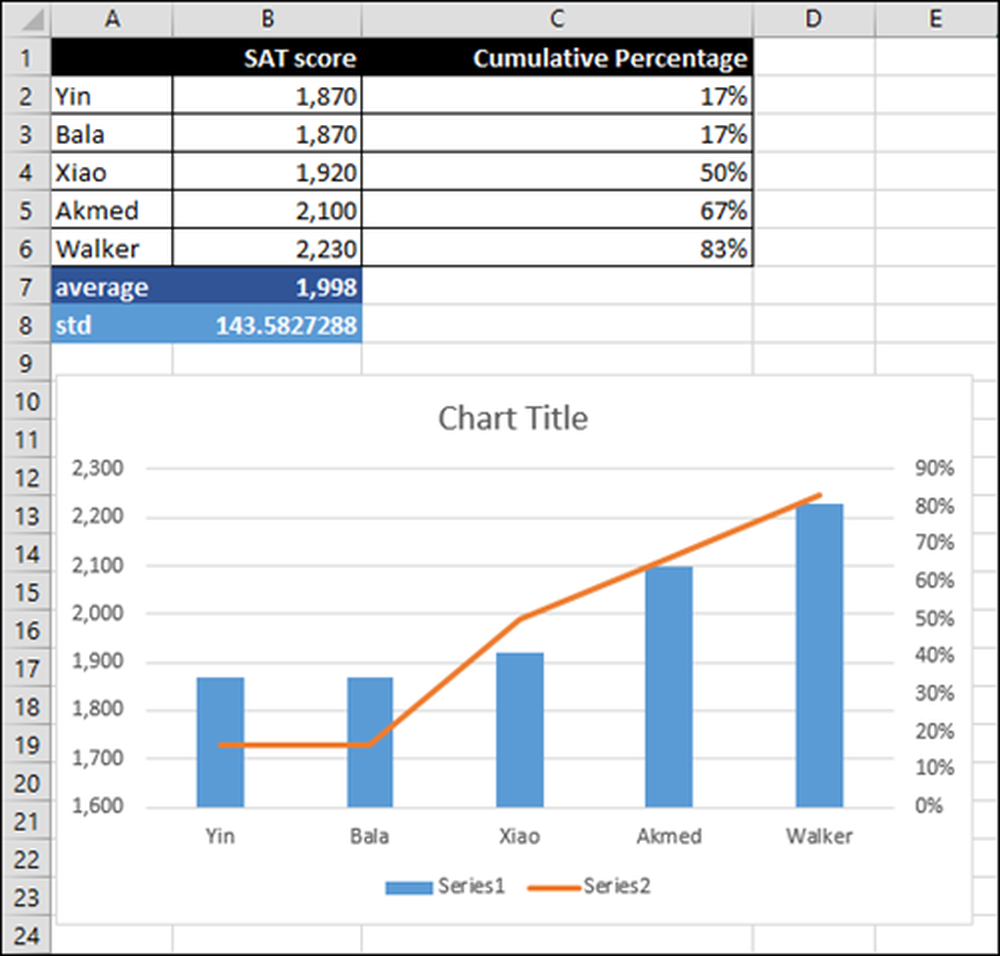
Om du högerklickar på diagrammet, väljer du "Välj data", vilken data som valts för intervallet.

Funktionen "Rekommenderade diagram" brukar vanligtvis hävda dig från att hantera så komplicerade detaljer som att bestämma vilken data som ska inkluderas, hur man tilldelar etiketter och hur man tilldelar vänster och höger vertikala axlar.

I dialogrutan "Välj datakälla" klickar du på "poäng" under "Legend Entries (Series)" och trycker på "Redigera" och ändrar det för att säga "Score."

Ändra sedan serie 2 ("percentil") till "Percentile".

Återgå till ditt diagram och klicka på "Chart Title" och ändra det till "SAT Scores." Nu har vi ett komplett diagram. Den har två horisontella axlar: en för SAT-poäng (blå) och en för kumulativ procentandel (orange).

Exempel: Transportproblemet

Transportproblemet är ett klassiskt exempel på en typ av matematik som kallas "linjär programmering". Det här låter dig maximera eller minimera ett värdeobjekt med vissa begränsningar. Det har många applikationer till ett stort antal affärsproblem, så det är användbart att lära sig hur det fungerar.

Innan vi börjar med det här exemplet måste vi aktivera "Excel Solver".

Aktivera tilläggslösare

Välj "File" -> "Options" -> "Add-ins". Längst ned i tilläggsalternativen klickar du på knappen "Gå" bredvid "Hantera: Excel-tillägg".

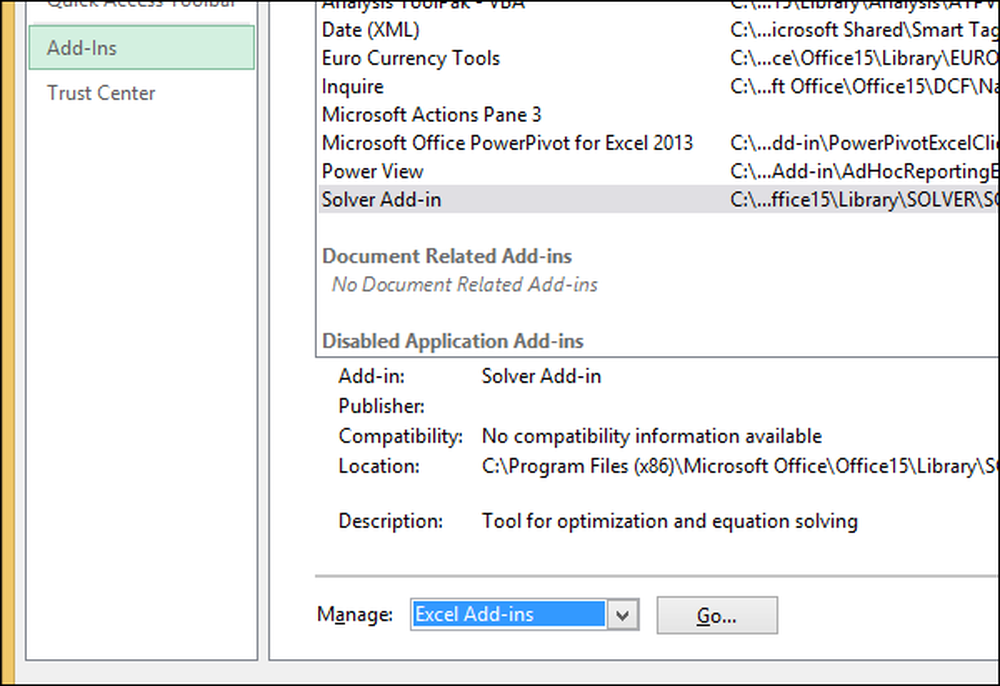
På den resulterande menyn klickar du på kryssrutan för att aktivera "Solver Add-in" och klicka på "OK".

Exempel: Beräkna de lägsta iPad-fraktkostnaderna

Antag att vi skickar iPads och vi försöker fylla våra distributionscenter med de lägsta transportkostnaderna. Vi har ett avtal med ett lastbil och flygbolag att skicka iPads från Shanghai, Beijing och Hong Kong till distributionscentra som visas nedan.

Priset för att skicka varje iPad är avståndet från fabriken till distributionscentralen till fabriken dividerat med 20.000 kilometer. Till exempel är det 8,024 km från Shanghai till Melbourne vilket är 8,024 / 20,000 eller $ .40 per iPad.

Frågan är hur vi skickar alla dessa iPads från dessa tre anläggningar till dessa fyra destinationer till lägsta möjliga kostnad?

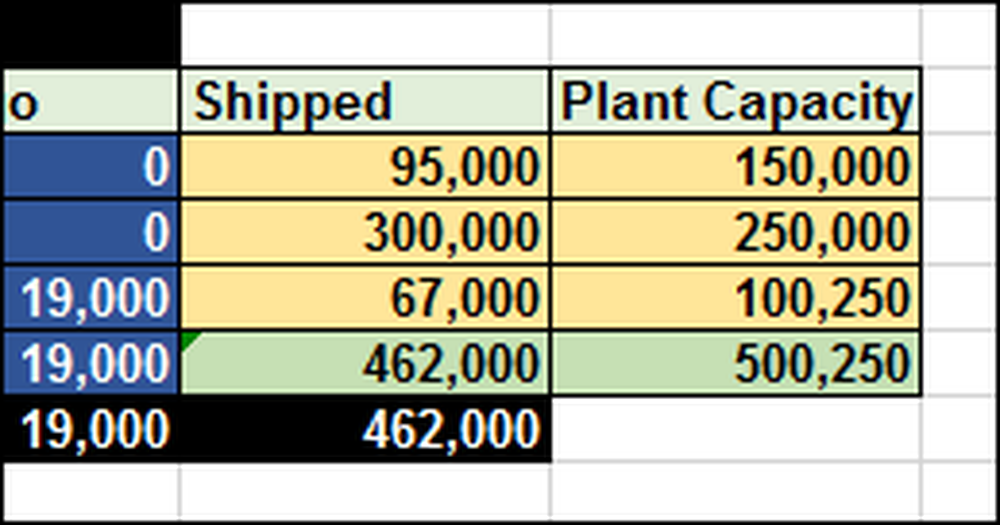
Som du kan föreställa dig, kan det här vara mycket svårt att räkna ut utan någon formel och verktyg. I det här fallet måste vi skicka 462 000 (F12) totalt iPads. Växterna har en begränsad kapacitet på 500 250 (G12) enheter.

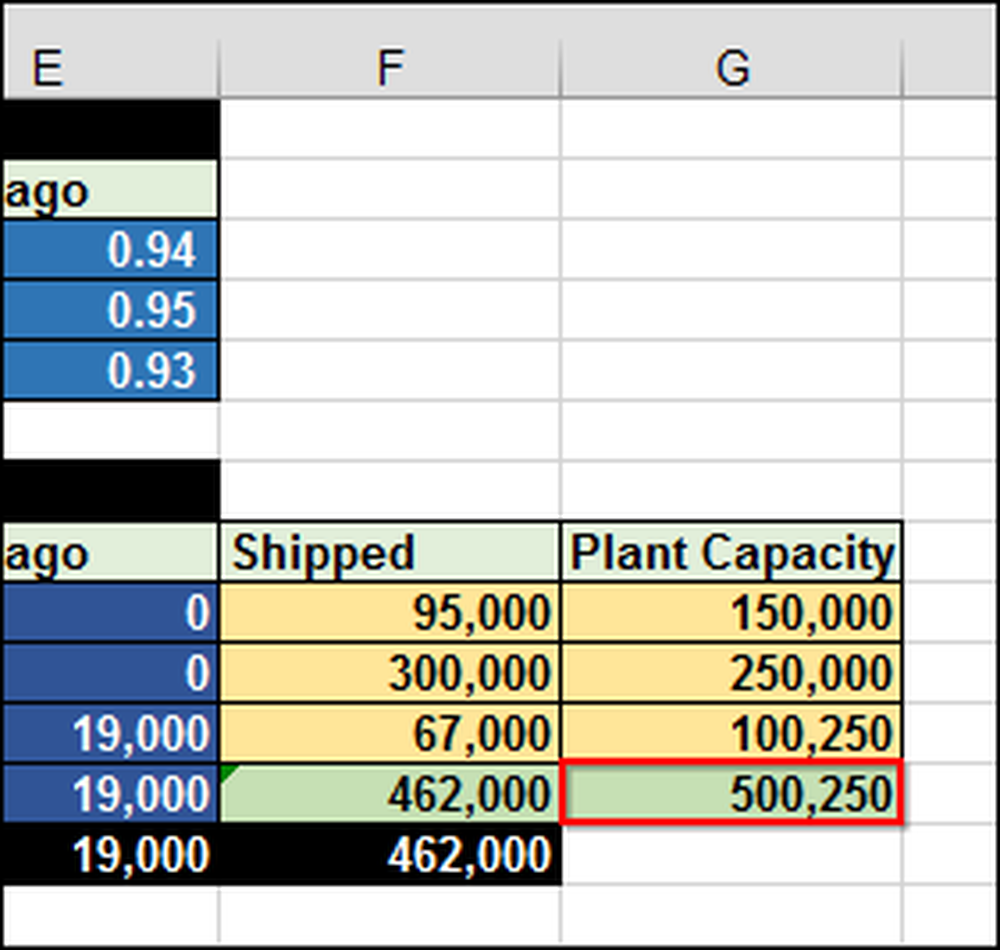
I kalkylbladet, så att du kan se hur det fungerar, har vi skrivit 1 till cell B10 vilket innebär att vi vill skicka en iPad från Shanghai till Melbourne. Eftersom transportkostnader längs den vägen är $ 0,40 per iPad är den totala kostnaden (B17) $ 0,40.

Numret beräknades med funktionen = SUMPRODUCT (kostnader, levereras) "kostnader" är intervall B3: E5.

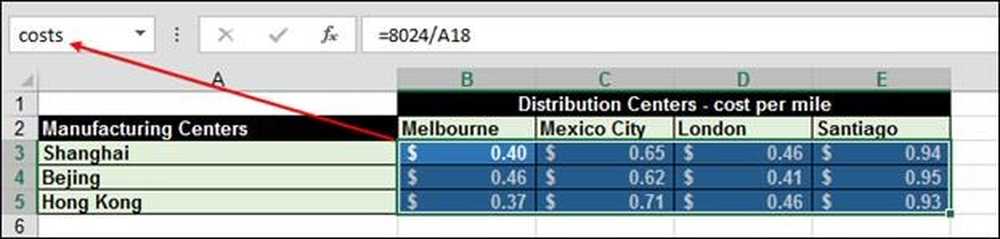
Och "levereras" är intervallet B9: E11:

SUMPRODUCT multiplicerar "kostnader" gånger intervallet "skickat" (B14). Det kallas "matrisförökning".

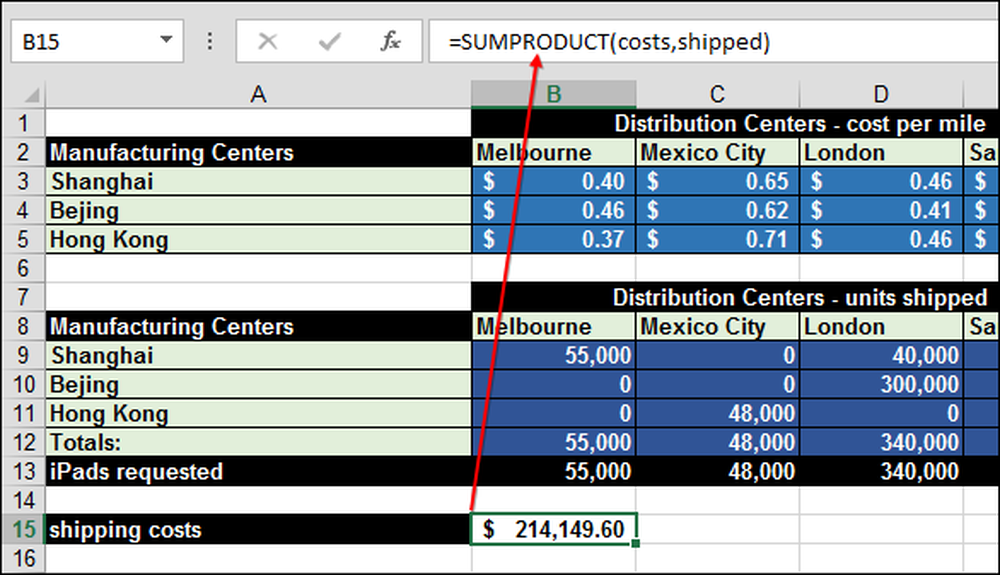
För att SUMPRODUCT ska fungera korrekt måste de två matriserna - kostnader och leveranser - vara lika stora. Du kan komma runt denna begränsning genom att göra extra kostnader och fraktkolumner och rader med nollvärde så att arraysna är lika stora och det påverkar inte de totala kostnaderna.

Använda lösaren

Om allt vi behövde var att multiplicera matriserna "kostnader" gånger "levereras", det skulle inte vara för komplicerat, men vi måste också hantera begränsningar där.

Vi måste skicka vad varje distributionscenter kräver. Vi lägger det konstant i lösaren så här: $ B $ 12: $ E $ 12> = $ B $ 13: $ E $ 13. Detta betyder summan av vad som skickas, dvs summan i celler $ B $ 12: $ E $ 12, måste vara större än eller lika med vad varje distributionscenter kräver ($ B $ 13: $ E $ 13).

Vi kan inte leverera mer än vi producerar. Vi skriver de här begränsningarna så här: $ F $ 9: $ F $ 11 <= $G$9:$G$11. Put another way, what we ship from each plant $F$9:$F$11 cannot exceed (must be less than or equal to) the capacity of each plant: $G$9:$G$11.

Gå nu till "Data" -menyn och tryck på "Solver" -knappen. Om "Solver" -knappen inte finns, måste du aktivera tillägget Solver.

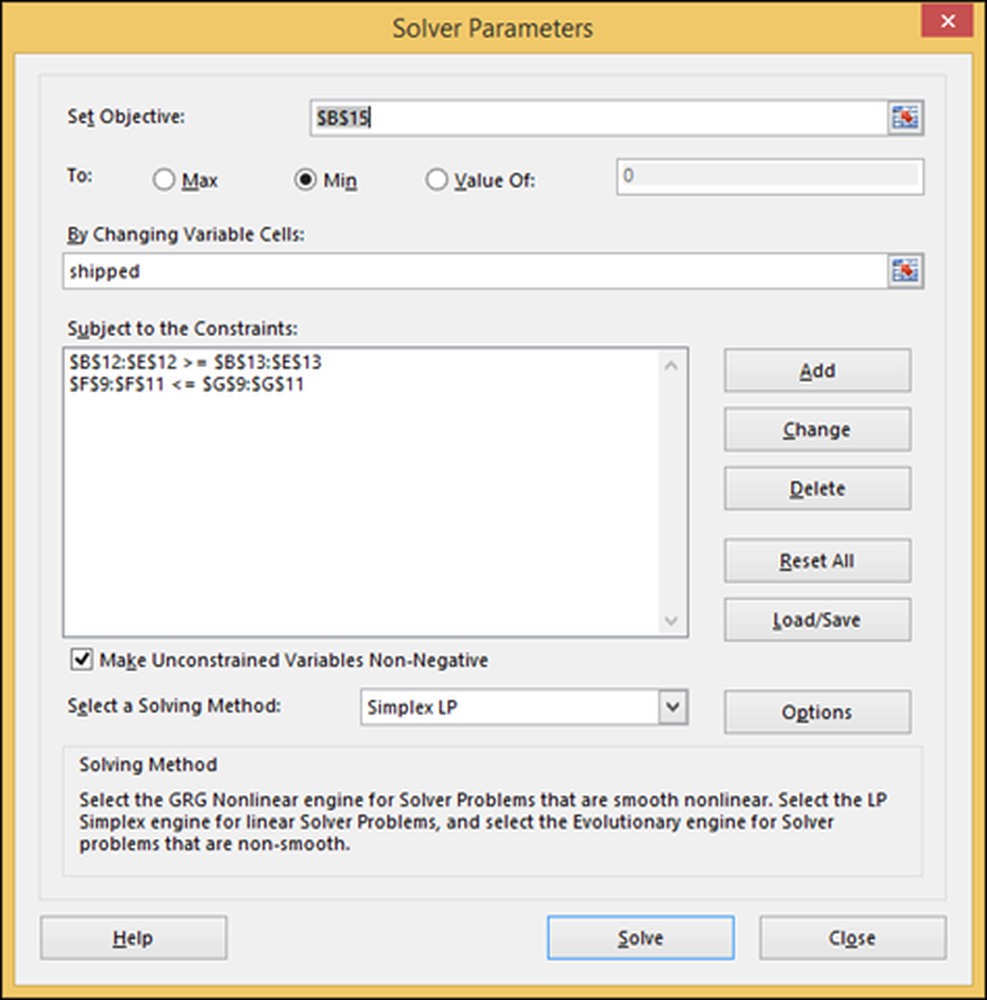
Skriv in de två begränsningarna som beskrivits tidigare och välj "Sändnings" -intervallet, vilket är det antal nummer som vi vill ha Excel att beräkna. Välj även standard algoritmen "Simplex LP" och ange att vi vill "minimera" cellen B15 ("totala fraktkostnader"), där det står "Set Objective."

Tryck på "Lös" och Excel sparar resultaten i kalkylbladet, vilket är vad vi vill ha. Du kan också spara det så att du kan leka med andra scenarier.

Om datorn säger att den inte kan hitta en lösning, har du gjort något som inte är logiskt, till exempel kan du ha begärt mer iPads än plantorna kan producera.

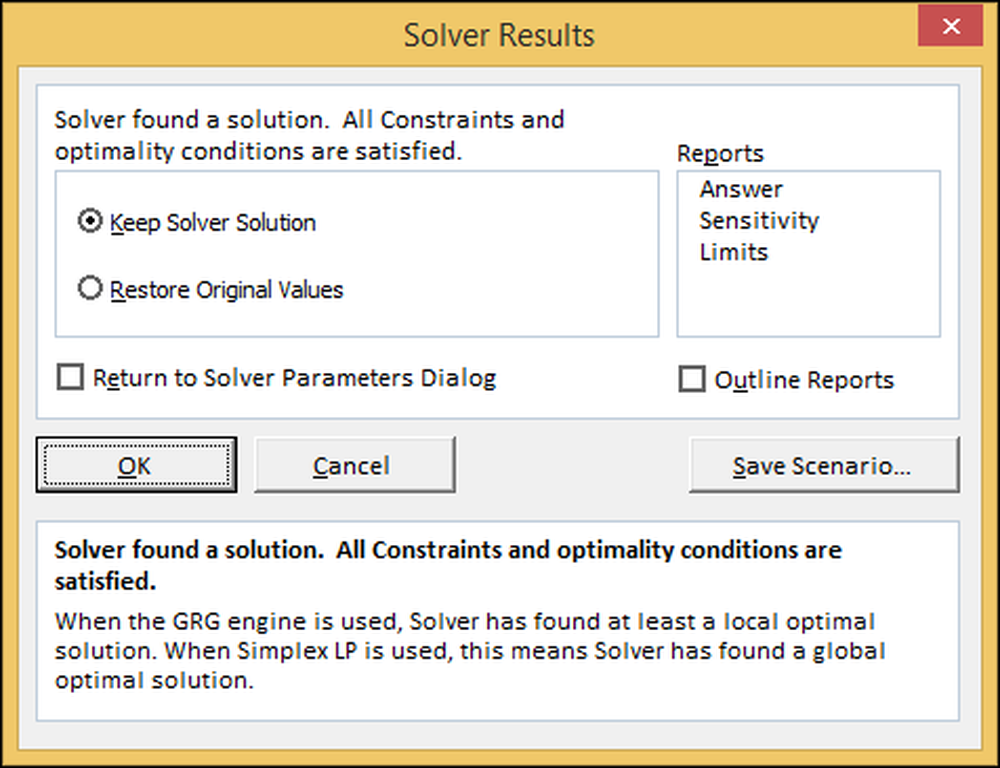
Här säger Excel att den har hittat en lösning. Tryck på "OK" för att hålla lösningen och återgå till kalkylbladet.

Exempel: Netto nuvärde

Hur bestämmer ett företag om man ska investera i ett nytt projekt? Om "Netto nuvärdet" (NPV) är positivt, kommer de att investera i det. Detta är ett standardinriktat tillvägagångssätt som tagits av de flesta finansiella analytiker.

Antag att Codelco-gruvföretaget vill utvidga Andinas kopparmruva. Standardmetoden för att bestämma huruvida man ska gå vidare med ett projekt är att beräkna nuvärdet. Om NPV är större än noll, blir projektet lönsamt med tanke på två insatser (1) tid och (2) kapitalkostnad.

På vanlig engelska betyder kostnaden för kapital hur mycket pengarna skulle tjäna om de bara lämnade det i banken. Du använder kapitalkostnaden för att diskontera kontantvärden till nuvarande värde, med andra ord kan $ 100 på fem år vara $ 80 idag.

Under det första året avsätts 45 miljoner dollar för att finansiera projektet. Revisorerna har bestämt att deras kapitalkostnad är sex procent.

När de börjar gruva börjar pengarna komma in, eftersom företaget hittar och säljer koppar de producerar. Självklart ju ju mer de min, ju mer pengar de gör och deras prognos visar att deras kassaflöde ökar tills det når 9 miljoner dollar per år.

Efter 13 år är NPV $ 3 945 074 USD, så projektet kommer att vara lönsamt. Enligt Finansanalytiker är "återbetalningsperioden" 13 år.

Skapa ett pivottabell

Ett "svängbord" är i grunden en rapport. Vi kallar dem pivottabeller eftersom du enkelt kan byta dem en typ av rapport till en annan utan att behöva göra en helt ny rapport. Så de svänga på plats. Låt oss visa ett grundläggande exempel som lär ut de grundläggande begreppen.

Exempel: Försäljningsrapporter

Försäljningsfolk är mycket konkurrenskraftiga (det är en del av att vara säljare) så de vill naturligtvis veta hur de går mot varandra i slutet av kvartalet och slutet av året, plus hur mycket sina provisioner kommer att bli.

Antag att vi har tre säljare - Carlos, Fred och Julie - alla säljer petroleum. Deras försäljning i dollar per skattekvartal för år 2014 visas i kalkylbladet nedan.

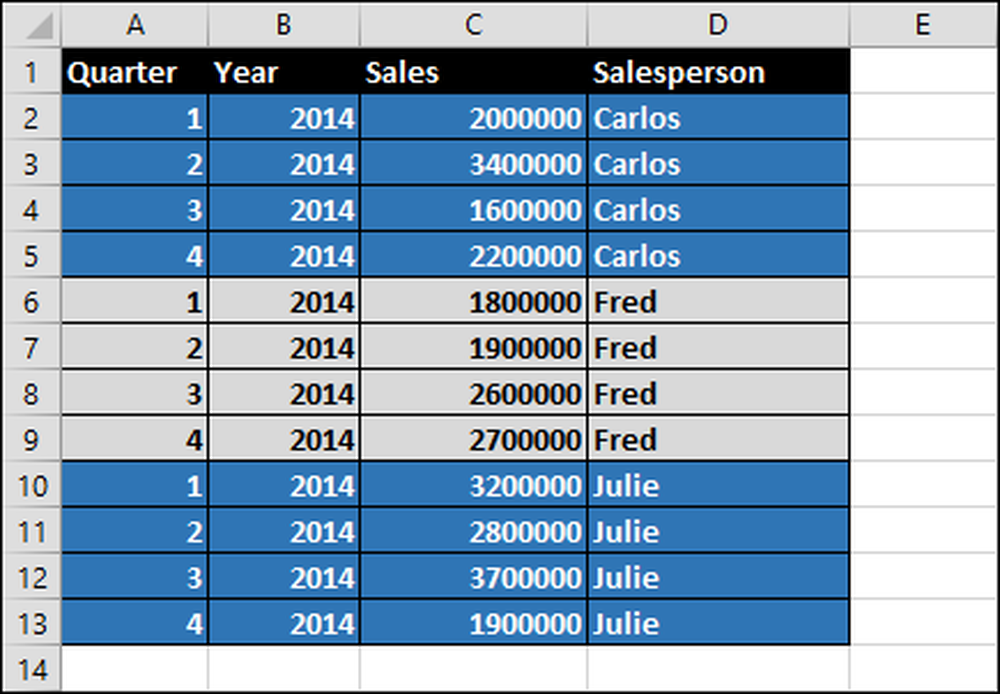
För att generera dessa rapporter skapar vi ett pivottabell:

Välj "Insert -> Pivot Table, det är på vänster sida av verktygsfältet:

Välj alla rader och kolumner (inklusive försäljarens namn) enligt nedan:

Dialogrutan för pivottabellen visas till höger om kalkylbladet.

Om vi ​​klickar på alla fyra fälten i pivottabelldialogrutan (kvartalet, året, försäljningen och säljaren) lägger Excel till en rapport i kalkylbladet som inte har någon mening men varför?

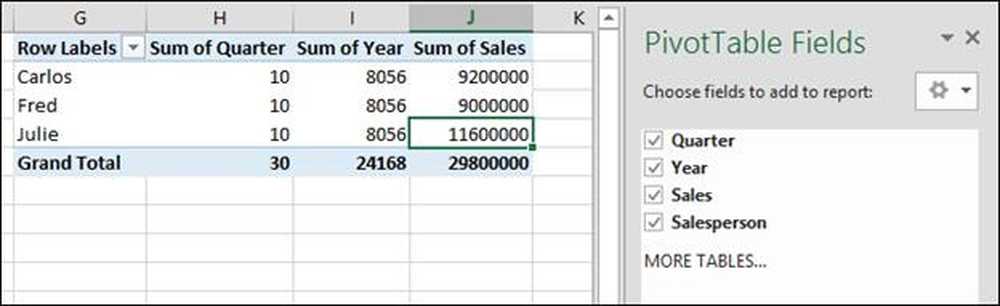
Som du kan se har vi valt alla fyra fält att lägga till i rapporten. Excels standardbeteende är att gruppera rader genom textfält och summera sedan resten av raderna.

Här ger vi oss summan av 2014 + 2014 + 2014 + 2014 = 24 168, vilket är nonsens. Det gav också summan av kvartalen 1 + 2 + 3 + 4 = 10 * 3 = 3 0. Vi behöver inte denna information, så vi avmarkerar dessa fält för att ta bort dem från vårt pivottabell.

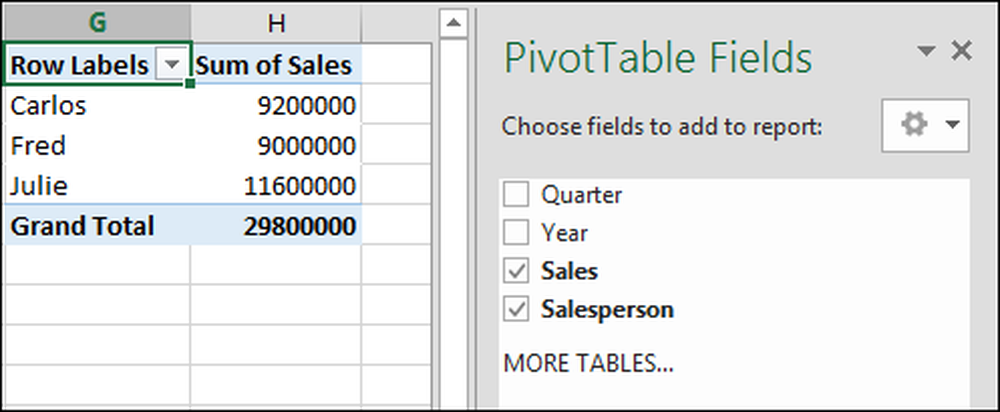
Summan av försäljningen (total försäljning) är emellertid relevant, så vi fixar det.

Exempel: Försäljning av försäljare

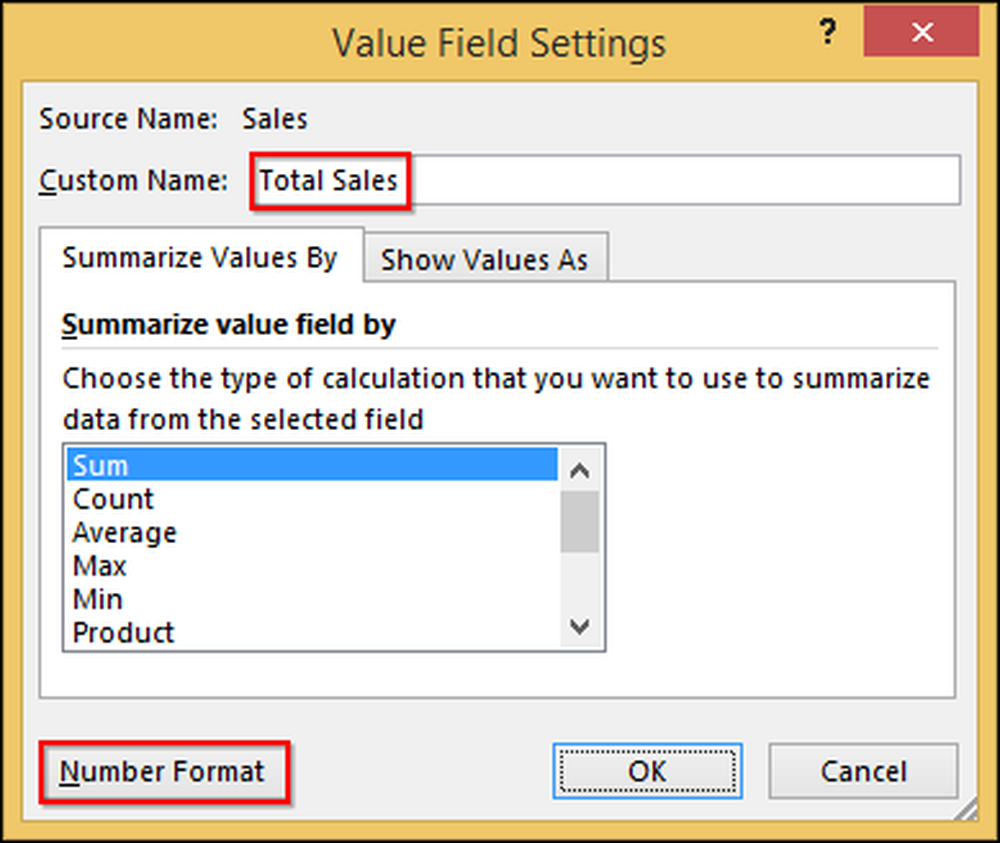
Du kan redigera "Summan av försäljning" som säger "Total försäljning", vilket är tydligare. Du kan också formatera cellerna som valuta precis som du skulle formatera alla andra celler. Klicka först på "Summan av försäljning" och välj "Värdefältinställningar".

I den resulterande dialogrutan byter vi namnet till "Total försäljning" och klickar sedan på "Nummerformat" och ändrar det till "Valuta".

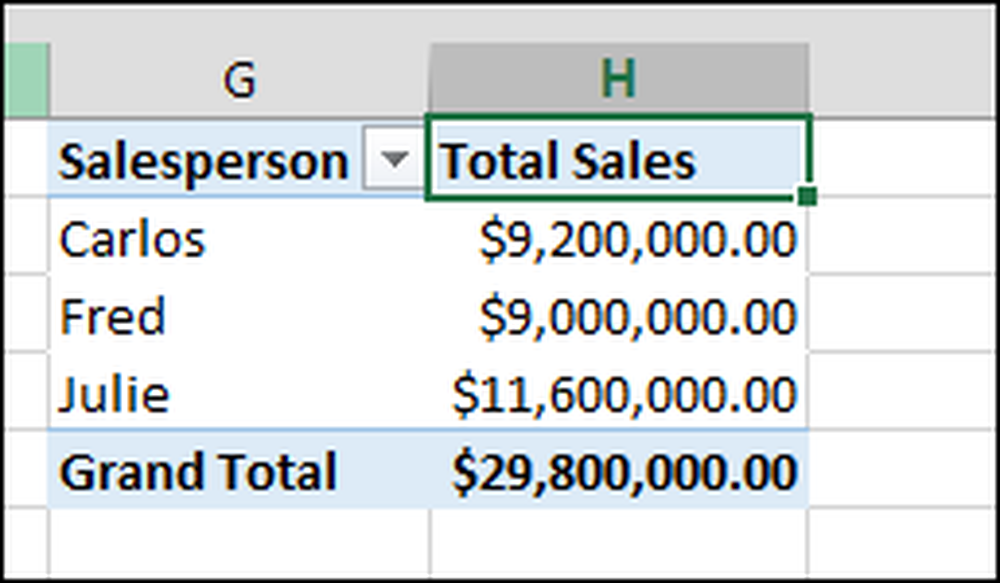
Du kan då se ditt handarbete i pivottabellen:

Exempel: Försäljning av försäljare och kvartal

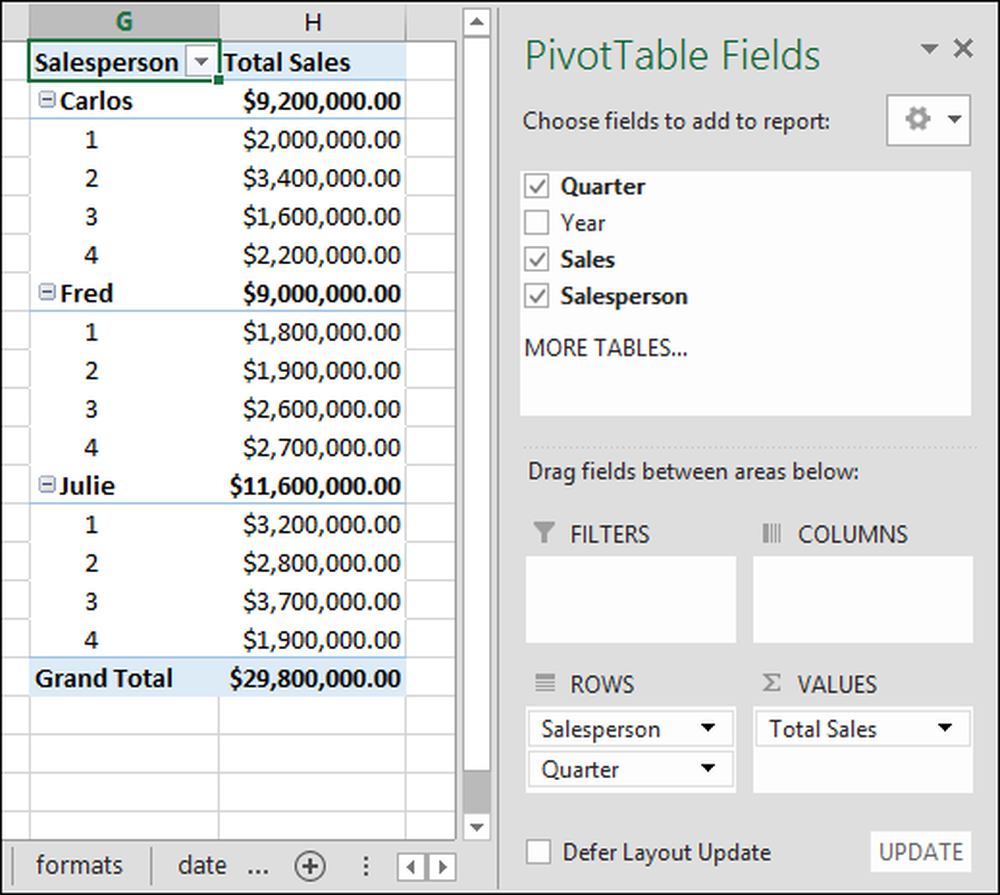
Låt oss nu lägga till subtotaler för varje kvartal. För att lägga till subtotaler bara vänster-klicka på "Kvartal" fältet och håll och dra det till "rader" sektionen. Du kan se resultatet på skärmdumpen nedan:

Medan vi är på det, låt oss ta bort värdet "Summa av kvartalet". Klicka bara på pilen och klicka på "Ta bort fält". I skärmbilden kan du nu se att vi har lagt till "Kvartals" raderna, vilket bryter ner varje säljare s försäljning per kvartal.

Med dessa färdigheter fräscha kan du nu skapa pivottabeller från dina egna data!

Slutsats

Inpakning, vi har visat dig några av funktionerna i Microsoft Excels formler och funktioner som du kan tillämpa Microsoft Excel på dina affärer, akademiska eller andra behov.

Som du har sett är Microsoft Excel en enorm produkt med så många funktioner att de flesta, även avancerade användare, inte känner till dem alla. Vissa människor kan säga att det gör det komplicerat; Vi anser att det är mer omfattande.

Förhoppningsvis har vi, genom att presentera massor av verkliga exempel, visat inte bara de funktioner som finns i Microsoft Excel men har lärt dig något om statistik, linjär programmering, skapa diagram, använda slumpmässiga nummer och andra idéer som du nu kan anta och Använd i din skola eller var du arbetar.

Kom ihåg att om du vill gå tillbaka och ta kursen igen, kan du börja fräscha med lektion 1!