Hur man beräknar en Z-poäng med hjälp av Microsoft Excel

En Z-Poäng är ett statistiskt värde som berättar hur många standardavvikelser ett visst värde hinner vara från medelvärdet av hela datasatsen. Du kan använda AVERAGE- och STDEV.S- eller STDEV.P-formlerna för att beräkna medel- och standardavvikelsen för dina data och sedan använda dessa resultat för att bestämma Z-poängen för varje värde.

Vad är en Z-poäng och vad gör funktionerna AVERAGE, STDEV.S och STDEV.P?

En Z-poäng är ett enkelt sätt att jämföra värden från två olika datasatser. Det definieras som antalet standardavvikelser bort från det medelvärde en datapunkt ligger. Den allmänna formeln ser så här ut:

= (Datapoint-AVERAGE (DataSet)) / STDEV (DataSet)

Här är ett exempel som hjälper till att klargöra. Säg att du ville jämföra testresultaten från två algebrastudenter undervisade av olika lärare. Du vet att den första studenten fick 95% på slutprovet i en klass, och studenten i den andra klassen gjorde 87%.

Vid första anblicken är 95% -graden mer imponerande, men vad händer om läraren i andra klassen gjorde en svårare examen? Du kan beräkna Z-poängen för varje elevs poäng baserat på genomsnittliga poäng i varje klass och standardavvikelsen för poängen i varje klass. Att jämföra Z-poängen för de två eleverna kunde avslöja att studenten med 87% poängen gjorde bättre i jämförelse med resten av sin klass än den student med 98% poängen gjorde i jämförelse med resten av sin klass.

Det första statistiska värdet du behöver är "mean" och Excels "AVERAGE" -funktion beräknar det värdet. Det lägger helt enkelt upp alla värden i ett cellintervall och delar upp summan av antalet celler som innehåller numeriska värden (det ignorerar tomma celler).

Det andra statistiska värdet vi behöver är "standardavvikelsen" och Excel har två olika funktioner för att beräkna standardavvikelsen på något olika sätt.

Tidigare versioner av Excel hade bara "STDEV" -funktionen, som beräknar standardavvikelsen medan data behandlas som ett "prov" för en befolkning. Excel 2010 bröt det i två funktioner som beräknar standardavvikelsen:

STDEV.S: Denna funktion är identisk med föregående "STDEV" -funktion. Det beräknar standardavvikelsen medan data behandlas som ett "prov" för en befolkning. Ett urval av en befolkning kan vara ungefär som de speciella myggor som samlats in för ett forskningsprojekt eller bilar som ställdes åt sidan och användes för kollisionssäkerhetsprovning.
STDEV.P: Denna funktion beräknar standardavvikelsen medan data behandlas som hela befolkningen. En hel befolkning skulle vara något som alla myggor på jorden eller varje bil i en produktionsdrift av en viss modell.

Vilket du väljer är baserat på din dataset. Skillnaden är vanligen liten, men resultatet av funktionen "STDEV.P" kommer alltid att vara mindre än resultatet av "STDEV.S" -funktionen för samma dataset. Det är ett mer konservativt tillvägagångssätt att anta att det finns mer variation i data.

Låt oss titta på ett exempel

För vårt exempel har vi två kolumner ("Värderingar" och "Z-poäng") och tre "hjälpar" -celler för att lagra resultaten av funktionerna "AVERAGE", "STDEV.S" och "STDEV.P". Kolumnen "Värden" innehåller tio slumptal centrerade runt 500 och kolumnen "Z-poäng" är där vi kommer att beräkna Z-poäng med resultaten som lagras i "hjälparcellerna".

Först ska vi beräkna medelvärdet av värdena med funktionen "AVERAGE". Välj den cell där du kommer att lagra resultatet av funktionen "AVERAGE".

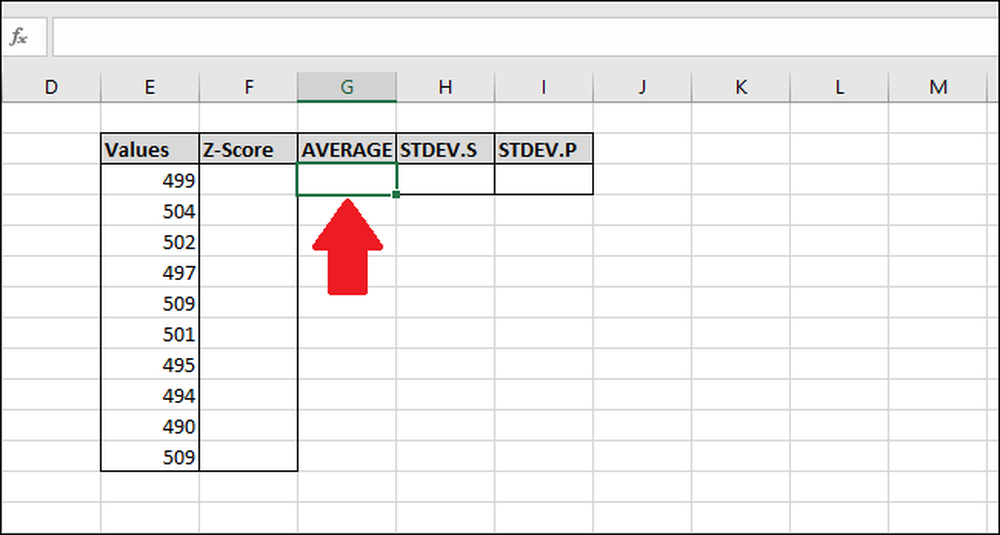
Skriv in följande formel och tryck på stiga på -eller använd menyn "Formler".

= MEDEL (E2: E13)

För att komma åt funktionen via "Formler" -menyn, välj rullgardinsmenyn Fler funktioner, välj alternativet "Statistiskt" och klicka sedan på "AVERAGE".

I fönstret Funktionsargument markerar du alla celler i kolumnen "Värden" som inmatning för fältet Nummer1. Du behöver inte oroa sig för "Number2" -fältet.

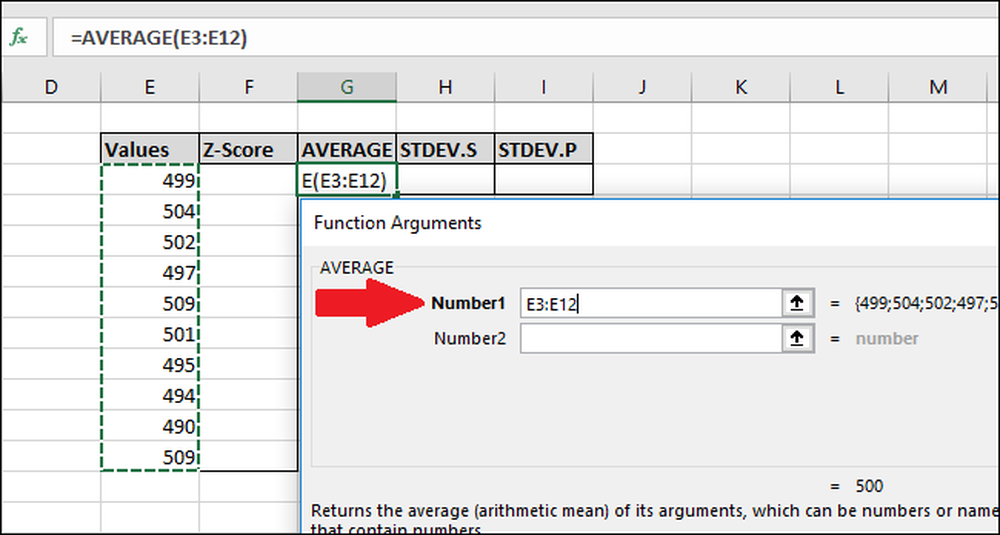
Tryck nu på "OK".

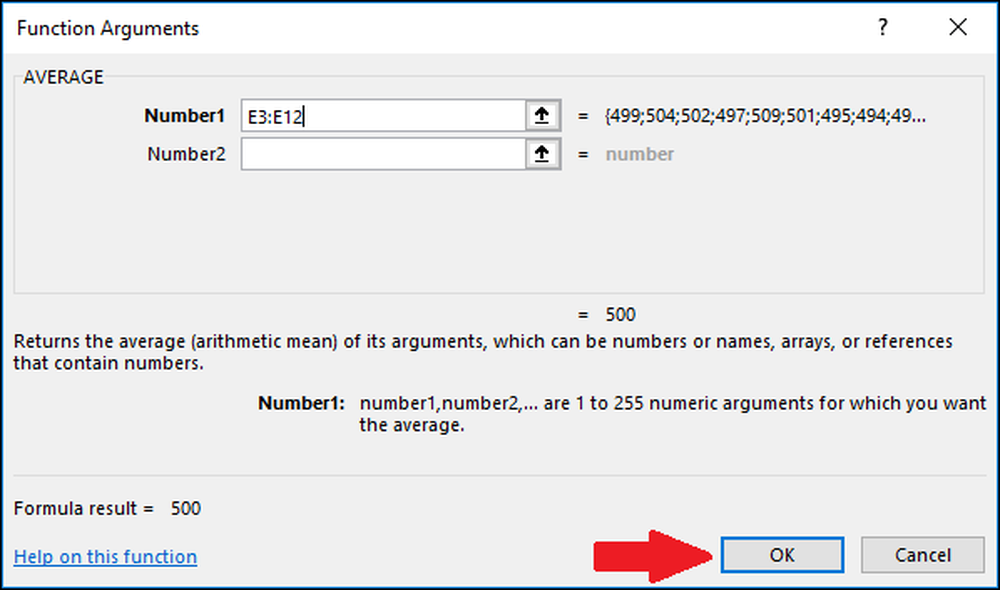
Därefter måste vi beräkna standardavvikelsen för värdena med antingen funktionen "STDEV.S" eller "STDEV.P". I det här exemplet kommer vi att visa hur du beräknar båda värdena, börjar med "STDEV.S." Välj den cell där resultatet kommer att lagras.

För att beräkna standardavvikelsen med funktionen "STDEV.S" skriver du in denna formel och trycker på Enter (eller öppnar den via menyn "Formler").

= STDEV.S (E3: E12)

För att komma åt funktionen via "Formler" -menyn, välj rullgardinsmenyn "Fler funktioner", välj alternativet "Statistiskt", rulla ner en bit och klicka sedan på "STDEV.S" -kommandot.

I fönstret Funktionsargument markerar du alla celler i kolumnen "Värden" som inmatning för fältet Nummer1. Du behöver inte oroa dig för "Number2" -fältet här heller.

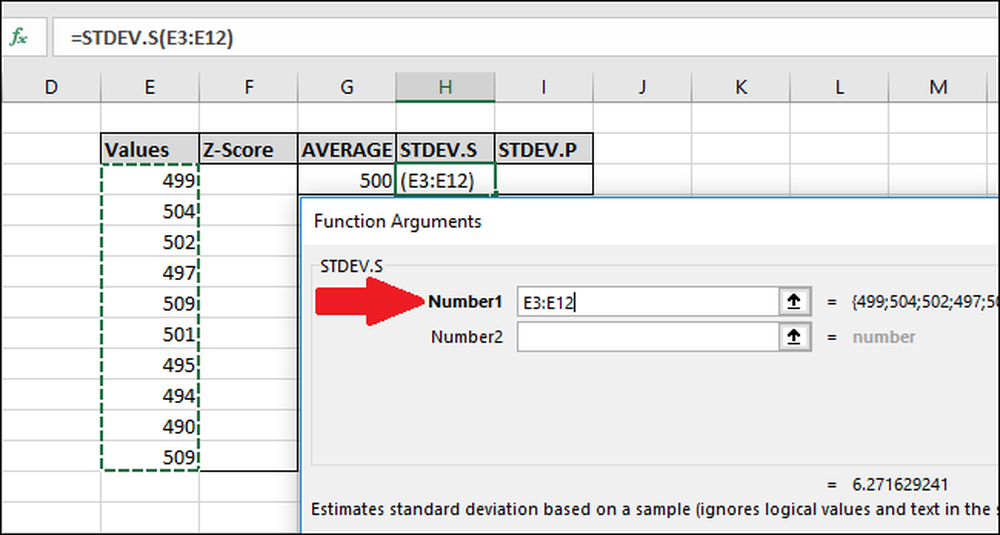
Tryck nu på "OK".

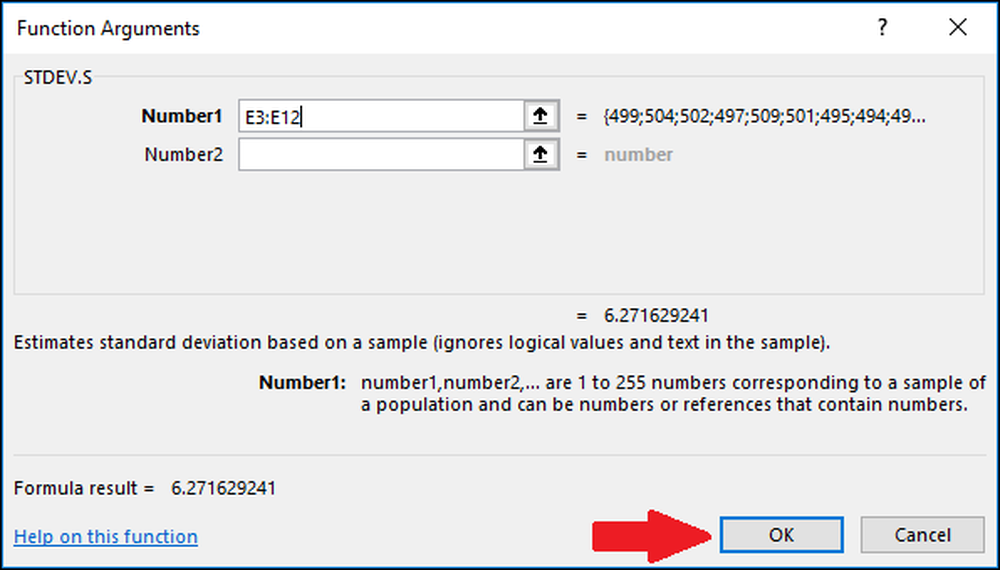
Därefter kommer vi att beräkna standardavvikelsen med funktionen "STDEV.P". Välj den cell där resultatet kommer att lagras.

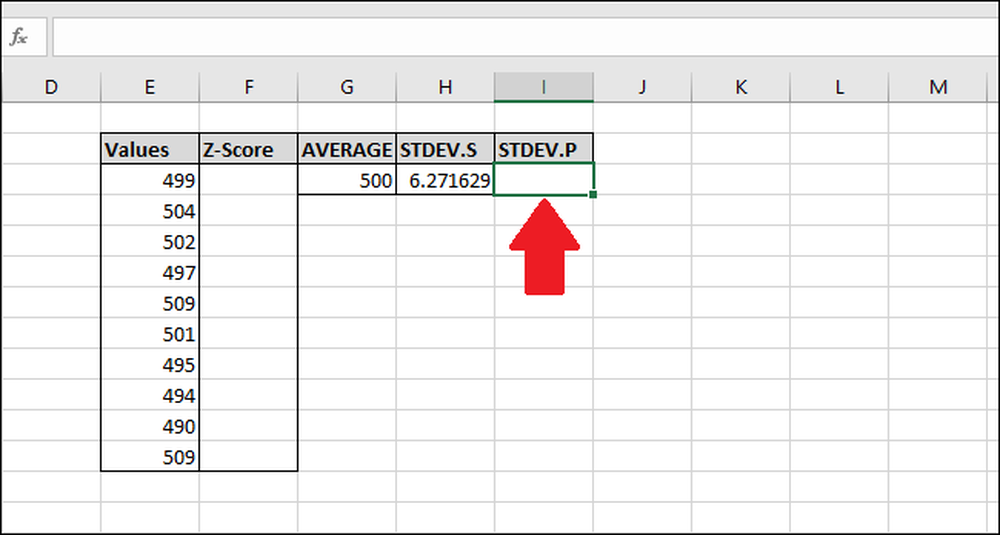
För att beräkna standardavvikelsen med funktionen "STDEV.P" skriver du in denna formel och trycker på Enter (eller öppnar den via menyn "Formler").

= STDEV.P (E3: E12)

För att komma åt funktionen via "Formler" -menyn, välj rullgardinsmenyn "Fler funktioner", välj alternativet "Statistiskt", rulla ner en bit och klicka sedan på "STDEV.P" -formeln.

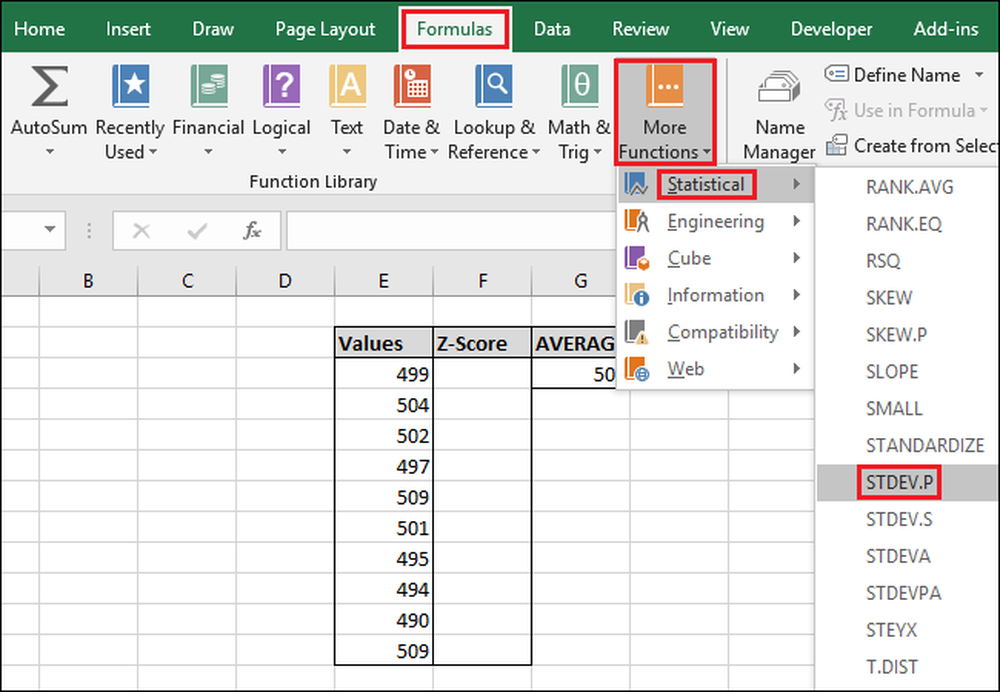
I fönstret Funktionsargument markerar du alla celler i kolumnen "Värden" som inmatning för fältet Nummer1. Återigen behöver du inte oroa dig för "Number2" -fältet.

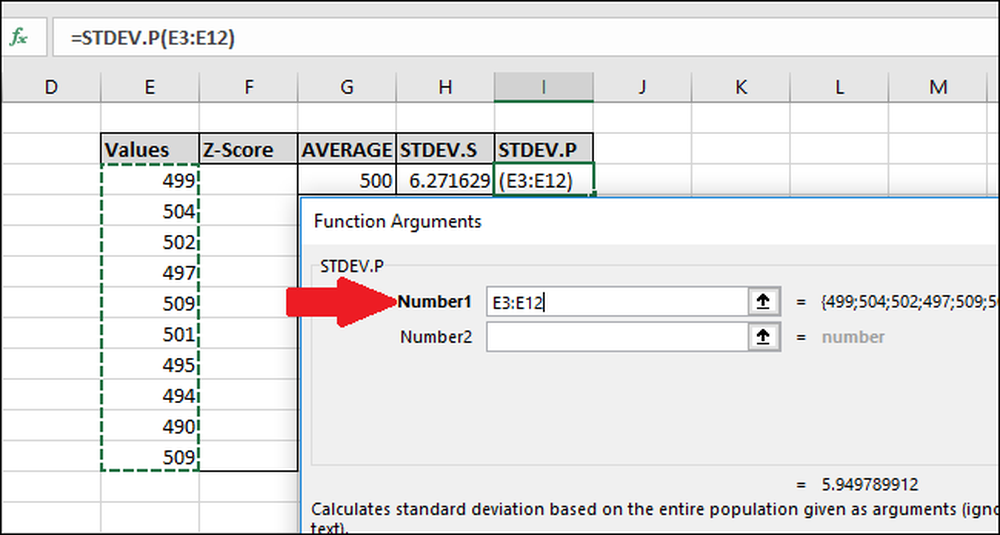
Tryck nu på "OK".

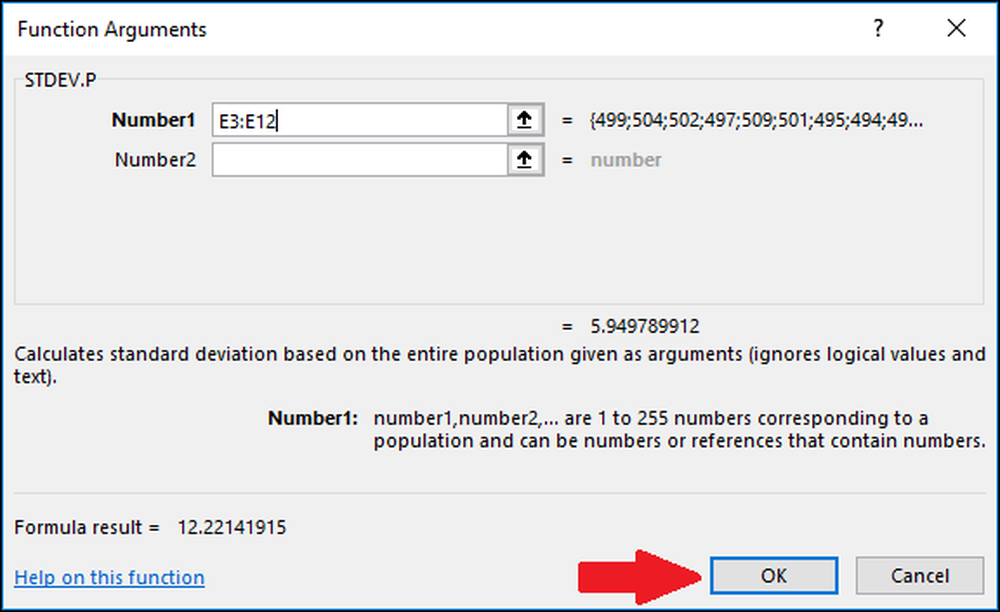
Nu när vi har beräknat medelvärdet och standardavvikelsen för våra data, har vi allt vi behöver för att beräkna Z-poängen. Vi kan använda en enkel formel som refererar till cellerna som innehåller resultaten av funktionerna "AVERAGE" och "STDEV.S" eller "STDEV.P".

Välj den första cellen i kolumnen "Z-poäng". Vi kommer att använda resultatet av funktionen "STDEV.S" för det här exemplet, men du kan också använda resultatet från "STDEV.P."

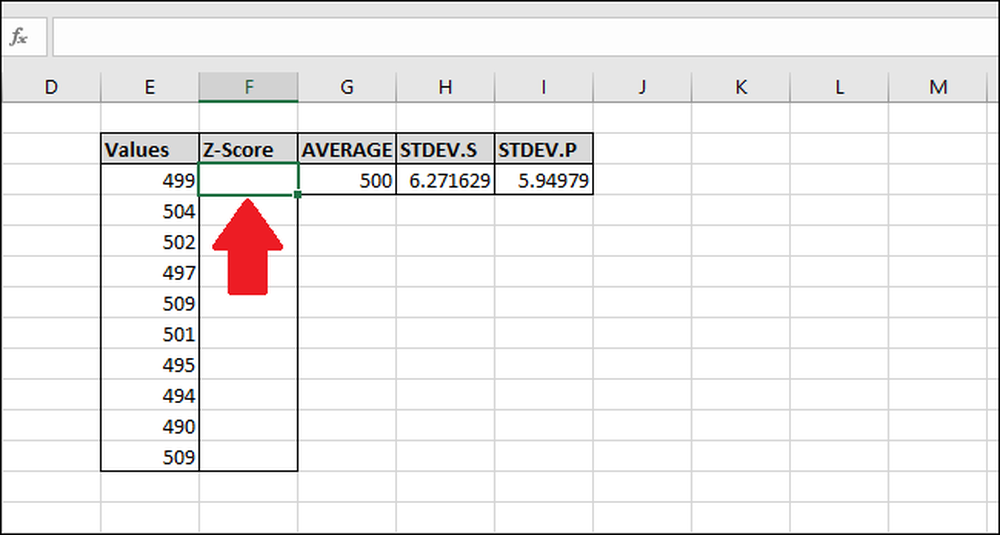
Skriv in följande formel och tryck på Enter:

= (E3 $ G $ 3) / $ H $ 3

Alternativt kan du använda följande steg för att ange formeln istället för att skriva:

Klicka på cell F3 och skriv = (
Välj cell E3. (Du kan trycka på vänster-pil-nyckel en gång eller använd musen)
Skriv minustecknet -
Välj cell G3 och tryck sedan på F4 att lägga till "$" tecken för att göra en "absolut" referens till cellen (den kommer att cykla genom "G3"> "$G$3 ">" G$3 ">"$G3 ">" G3 "om du fortsätter att trycka F4)
Typ ) /
Välj cell H3 (eller I3 om du använder "STDEV.P") och tryck på F4 för att lägga till de två "$" tecknen.
tryck enter

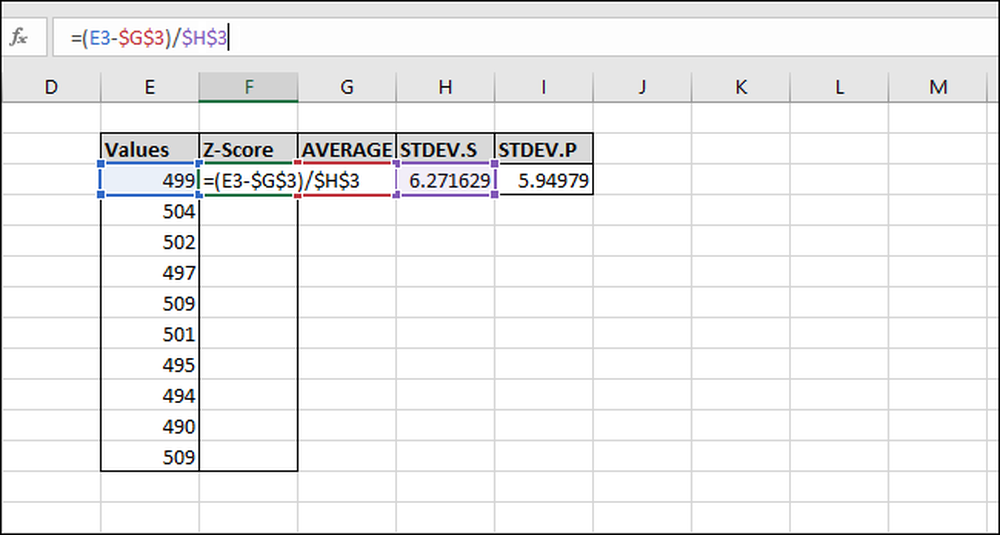
Z-poängen har beräknats för det första värdet. Det är 0,155945 standardavvikelser under medelvärdet. För att kontrollera resultaten kan du multiplicera standardavvikelsen enligt detta resultat (6.271629 * -0.15945) och kontrollera att resultatet är lika med skillnaden mellan värdet och medelvärdet (499-500). Båda resultaten är lika, så värdet är vettigt.

Låt oss beräkna Z-poängen för resten av värdena. Markera hela kolumnen Z-poäng som börjar med cellen som innehåller formeln.

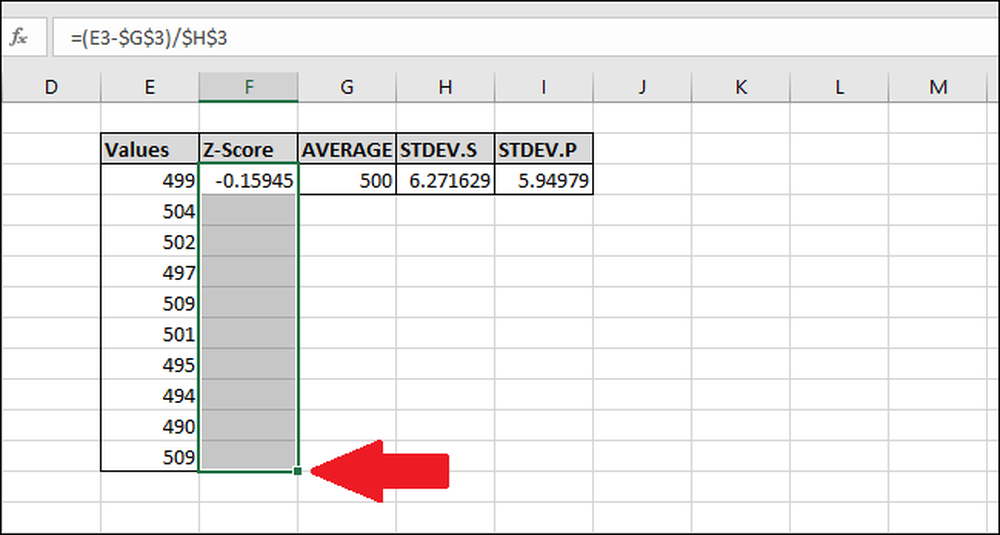
Tryck Ctrl + D, som kopierar formeln i den övre cellen ner genom alla andra valda celler.

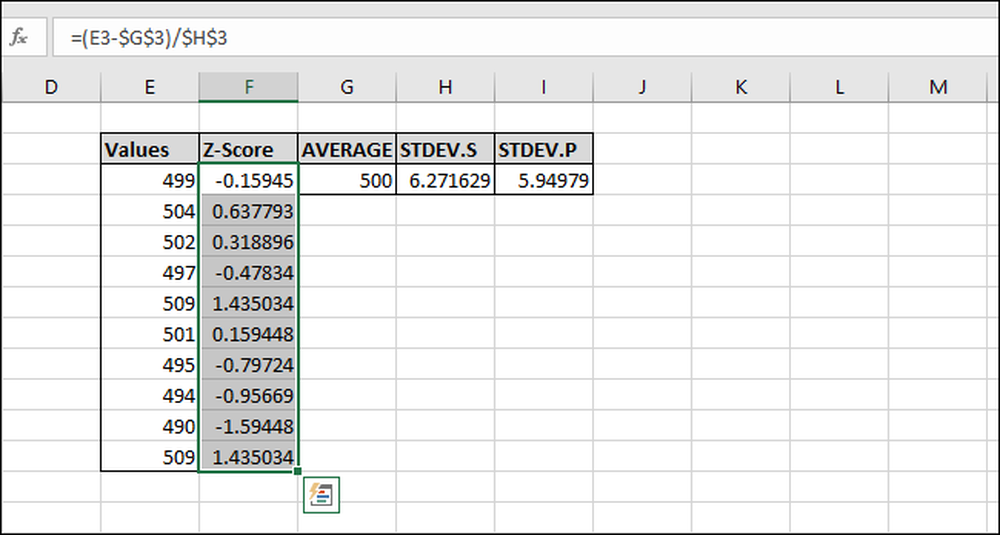
Nu har formeln blivit "fylld" till alla celler, och var och en refererar alltid till de korrekta "AVERAGE" och "STDEV.S" eller "STDEV.P" -cellerna på grund av "$" -tecknen. Om du får fel, gå tillbaka och se till att "$" -tecknen ingår i den formel du skrev in.

Beräkning av Z-poäng utan att använda "hjälpar" celler

Hjälpceller lagrar ett resultat, som de som lagrar resultaten av funktionerna "AVERAGE", "STDEV.S" och "STDEV.P". De kan vara användbara men är inte alltid nödvändiga. Du kan hoppa över dem helt när du beräknar en Z-poäng genom att använda följande generaliserade formler, istället.

Här är en som använder funktionen "STDEV.S":

= (Value-AVERAGE (Värden)) / STDEV.S (Values)

Och en som använder funktionen "STEV.P":

= (Value-AVERAGE (Värden)) / STDEV.P (Values)

När du anger cellområdena för värdena i funktionerna, var noga med att lägga till absoluta referenser ("$" med F4) så att när du fyller ner du inte beräknar genomsnittet eller standardavvikelsen i ett annat område av celler i varje formel.

Om du har en stor dataset kan det vara effektivare att använda hjälpceller eftersom det inte beräknar resultatet av funktionerna "AVERAGE" och "STDEV.S" eller "STDEV.P" varje gång, vilket sparar processorresurser och påskynda den tid det tar att beräkna resultaten.

Dessutom tar "$ G $ 3" färre byte att spara och mindre RAM att ladda än "AVERAGE ($ E $ 3: $ E $ 12).". Detta är viktigt eftersom standard 32-bitarsversion av Excel är begränsad till 2 GB RAM (64-bitarsversionen har inga begränsningar för hur mycket RAM som kan användas).